A de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring.
For a de Bruijn sequence of order n on a size-k alphabet $A$, we denote it by $B(k, n)$
Basic Properties
- $B(k, n)$ has length $k^n$ (also the number of distinct strings of length n on A)
- De Bruijn sequences are optimally short with respect to the property of containing every string of length n exactly once
- The number of distinct de Bruijn sequences $B(k, n)$ is
$$\frac{(k!)^{k^{n-1}}}{k^n}$$
An Example Sequence
let’s use $B(2, 4)$ as an example
Sequence 0000111101100101 (cyclic sequcence) belongs to $B(2,4)$.
It contains every string of length n exactly once:
| |
How to Construct the Sequence
Can be constructed by taking an Eulerian cycle of an (n − 1)-dimensional de Bruijn graph: (Hierholzer’s Algorithm) A de Bruijn graph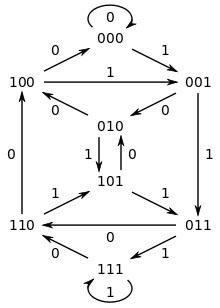
| |
Related Problems
leetcode 753: Cracking the Safe
example solution from leetcode discuss1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27class Solution { int n, k, v; vector<vector<bool> > visited; string sequence; public: string crackSafe(int n, int k) { if (k == 1) return string(n, '0'); this->n = n; this->k = k; v = 1; for (int i = 0; i < n - 1; ++i) v *= k; visited.resize(v, vector<bool>(k, false)); dfs(0); return sequence + sequence.substr(0, n - 1); } void dfs(int u) { for (int i = 0; i < k; ++i) { if (!visited[u][i]) { visited[u][i] = true; dfs((u * k + i) % v); sequence.push_back('0' + i); } } } };